Existen variados problemas en la vida diaria que llevan a desigualdades lineales.
El problema de la PROGRAMACION LINEAL que estudiaremos surgió en parte debido a la tecnología moderna en medicina, transporte, explotaciones forestales, agricultura, combustible, etc.
Los problemas de programación lineal del mundo real pueden tener
cientos y aun miles de variables. Sin embargo, inicialmente estudiaremos el caso de P.L. con 2 variables.
Obs: Todo problema de programación lineal trata de la maximización y minimización de una función lineal en el conjunto solución de un sistema formado por desigualdades o desigualad -des lineales. Para resolver un problema como el formulado antes,
consideramos la naturaleza de dichos conjuntos solución.
Obs: Cualquier desigualdad de la forma ax + by < c tiene como conjunto solución un semiplano formado por la recta ax+by=c
junto con la parte con la parte del plano que está a un lado de la recta. Dado cualquier sistema de desigualdades lineales con x e y, se desea hallar todos los puntos (x,y) para los cuales todos las desigualdades se cumplen simultáneamente.
Def:
El conjunto solución de un sistema de desigualdades lineales consiste en una intersección de estos semiplanos.
Ejemplo :
Sea el sistema de desigualdades lineales
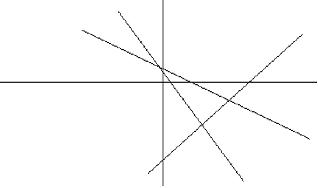
2x + 3y > 6
2x + y > 2
x - y < 3
Obs:
El conjunto solución no vacío de un sistema de desigualdades lineales lineales está acotado por rectas o segmentos de rectas y que todas sus esquinas apuntan hacia fuera. Dichos conjuntos se llaman conjuntos poligonales convexos.
Def:
Un subconjunto del plano es convexo si para cada par de ptos P y Q del conjunto el segmento de recta que los une también está en el conjunto
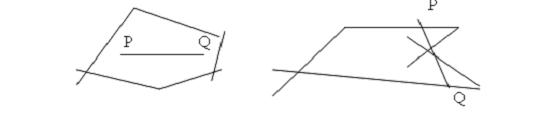
TEOREMA: Cualquier intersección no vacía de semiplanos es un conjunto convexo.
MAXIMIZAR Y MINIMIZAR ax +by EN UNE INTERSECCION DE SEMIPLANOS
Se considera el problema de programación lineal de maximizar o minimizar una función lineal ax + by en el conjunto solución de un sistema de desigualdades lineales. Las desigualdades se llaman restricciones y la función ax +by es la función objetivo.
Teniendo en cuenta las aplicaciones económicas a la función objetivo se le llama función de ganancia si se va a maximizar, y función de costo si se va a minimizar. En problemas aplicados siempre se considera que dos de las restricciones son x>0 e y>0.
El conjunto solución convexo de la restricciones se llama conjunto factible y cualquier punto de este conjunto es una solución factible. Nuestro fin será entonces determinar entre todas las soluciones factibles aquellas que maximicen o minimicen ax + by.
Supongamos que para una solución factible (x0,y0), y una función de costo ax+by tenemos ax0+by0 = c0. Entonces toda solución factible que esté en la recta ax + by = c también dá el mismo valor c0 para esta función de costo. Para una solución factible (x1,y1) que no este en esta recta, obtenemos algun costo c1, donde c1 = ax1 + by1, así todas las soluciones factibles (x,y) en la recta ax+by=c1 dan el mismo valor c1.
Las rectas ax + by = c0 y ax + by = c1 son paralelas .
Supongamos que su conjunto factible es
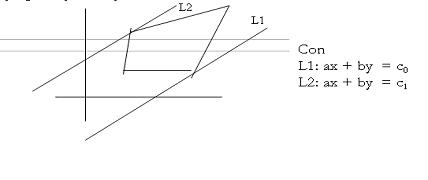
Si b> 0, el valor máximo C1 = Cmax es el valor de ax + by que esta en el último punto donde las rectas ax + by = c tocan al conjunto factible conforme C crece y las rectas se mueven hacia arriba. El valor mínimo Cmin = C0 se alcanza en el último punto donde las rectas tocan al conjunto conforme C decrece y las rectas se mueven hacia abajo.
Si b<0, las rectas se mueven hacia abajo conforme c crece, entonces los máximos y mínimos quedan de la siguiente forma
En este caso la posición final de la recta ax + by = c , antes de salir de un conjunto factible, coincida con todo un segmento frontera del conjunto.
Si el conjunto factible no es acotado entonces es posible que la función de costo no alcance máximo o mínimo. Si b>0, entonces ax+by no tiene máximo y si b<o se riene que ax+by no tiene mínimo
TEOREMA: Asunción del costo o ganancias optimales
Si una función objetivo lineal ax + by, asume un valor máximo en un conjunto definido por restricciones lineales, entonces este valor máximo se asume en un punto esquina del conjunto. Lo mismo sucede si una función objetivo asume un valor mínimo en el conjunto factible.
PROCEDIMIENTO PARA HALLAR MÁXIMO O MÍNIMO ALCANZADO POR UNA FUNCIÓN OBJETIVO AX+BY.
Hallar el máximo (mínimo) alcanzado por ax+by sujeto a un sistema de restricciones lineales.
Paso 1 : Esbozar el conjunto factible definido por las restricciones en un gráfico.
Paso 2: Determinar si es alcanzable un máximo o un mínimo.
CONTRUCCIÓN DE LOS MODELOS DE PROGRAMACIÓN LINEAL
De forma obligatoria se deben cumplir los siguientes requerimientos para construir un modelo de Programación Lineal.
- Requerimiento 1. Función objetivo. (F.O).
Debe haber un objetivo (o meta o blanco) que la optimización desea alcanzar.
- Requerimiento 2. Restricciones y decisiones.
Debe haber cursos o alternativas de acción o decisiones, uno de los cuáles permite alcanzar el objetivo.
- Requerimiento 3. La F.O y las restricciones son lineales.
Deben utilizarse solamente ecuaciones lineales o desigualdades lineales.
METODO ANALITICO O METODO DE LOS VERTICES
El siguiente resultado, denominado teorema fundamental de la programación lineal, nos permite conocer otro método de solucionar un programa con dos variables.
En un programa lineal con dos variables, si existe una solución única que optimice la función objetivo, ésta se encuentra en un punto extremo (vértice) de la región factible acotada, nunca en el interior de dicha región.
Si la función objetivo toma el mismo valor óptimo en dos vértices, también toma idéntico valor en los puntos del segmento que determinan.
En el caso de que la región factible no es acotada, la función lineal objetivo no alcanza necesariamente un valor óptimo concreto, pero, si lo hace, éste se encuentra en uno de los vértices de la región
La evaluación de la función objetivo en los vértices de la región factible nos va a permitir encontrar el valor óptimo (máximo o mínimo) en alguno de ellos.
Veámoslo con un ejemplo:
Maximizar Z = f(x,y) = 3x + 8y
sujeto a: 4x + 5y 40
2x + 5y 30
x 0 , y 0
1) Hallar los puntos de corte de las rectas asociadas a las restricciones:
Calculamos las soluciones de cada uno de los seis sistemas de dos ecuaciones con dos incógnitas que se pueden formar con las cuatro restricciones:
{ 4x + 5y = 40 , 2x + 5y = 30}. Solución A(5,4) { 4x + 5y = 40 , x = 0 } Solución:B (0,8)
{ 4x + 5y = 40 , y = 0}. Solución: C(10,0) { 2x + 5y = 30 , x = 0} Solución: D(0,6)
{ 2x + 5y = 30 , y = 0}. Solución : E(15,0) { x = 0, y = 0} Solución: O(0,0)
2) Determinar los vértices de la región factible:
Los vértices de la región factible son aquellos puntos que cumplen todas las restricciones.
Si sustituimos los puntos en cada una de las desigualdades tenemos que:
- B no cumple la segunda restricción 2x + 5y 30 , ya que 2·0 + 5·8 = 40 . Por tanto, el punto B no es un vértice de la región factible.
- E no cumple la primera restricción 4x + 5y 40 , ya que 4·15 + 5·0 = 60 . Por tanto, el punto E no es un vértice de la región factible.
Los puntos A, C, D y O verifican todas las desigualdades, son los vértices de la región factible.
3) Calcular los valores de la función objetivo en los vértices:
F(A) = f(5,4) = 3·5 + 8·4 = 47 f(C) = f(10,0) = 3·10 + 8· 0 = 30
F(D) = f(0,6) = 3·0 + 8·6 = 48 f(O) = f(0,0) = 3·0 + 8·0 = 0
La solución óptima corresponde al vértice para el que la función objetivo toma el valor máximo. En este caso es el vértice D(0,6).
PROBLEMA METODO ANALITICO
La Zamoempresa de Cultivos Extensivos produce maiz y sorgo. El doble de la producción de maiz es siempre menor o igual que la producción de sorgo más cuatro unidades. Por otra parte, el triple de la producción de sorgo sumado con cuatro veces la producción de maiz se mantiene siempre menor o igual a 18 unidades.
Halla el número de unidades de cada producto que se deben producir para alcanzar un beneficio máximo, sabiendo que cada unidad de maiz deja un beneficio de 8,00 Lempiras y cada unidad de sorgo de 2,00 Lempiras.
Planteamiento:
x--------maiz
y--------sorgo
2x<=y+4
3y+4x<=18
x>=0
y>=0
max: 8,00x+2,00y
Sistemas de Ecuaciones:
2x=y+4
3y+4x=18sol: (3,2) cumple con todas las restricciones
2x=y+4
x=0sol: (0,-4) no cumple con todas las restricciones
2x=y+4
y=0sol: (2,0) cumple con todas las restricciones
x=0
3y+4x=18sol: (0,6) cumple con todas las restricciones
y=0
3y+4x=18sol: (4.5,0) no cumple con todas las restricciones
Max(3, 2) = 2800
Mín(0, 0) = 0
Se deben producir 3 unidades de maiz a razon de 2 unidades de sorgo.
METODO GRAFICO O METODO DE LAS RECTAS DE NIVEL
Las rectas de nivel dan los puntos del plano en los que la función objetivo toma el mismo valor.
Si la función objetivo es f(x,y) = ax + by + c, la ecuación de las rectas de nivel es de la forma:
ax + by + c = 0 ax + by = k
Variando k (o p) se obtienen distintos niveles para esas rectas y, en consecuencia, distintos valores para f(x,y).
En un problema todas las rectas de nivel son paralelas, pues los coeficientes a y b de la recta ax + by = k son los que determinan su pendiente. Por tanto, si k1 es distinto de k2 , las rectas ax + by = k1 y ax + by = k2 son paralelas. Luego, trazada una cualquiera de esas rectas, las demás de obtienen por desplazamientos paralelos a ella.
Si lo que se pretende es resolver un problema de programación lineal, los únicos puntos que interesan son los de la región factible, y las únicas rectas de nivel que importan son aquellas que están en contacto con dicha región. Como el nivel aumenta (o disminuye) desplazando las rectas, el máximo (o el mínimo) de f(x,y) se alcanzará en el último (o en el primer) punto de contacto de esas rectas con la región factible.
Veamos ahora como se aplica todo esto a la resolución de un problema de programación lineal :
Maximizar Z = f(x,y) = x + y
sujeto a: 0 x 4
y x /2
1) Representamos la región factible:
- La recta s : x = 4 pasa por el punto (4,0) y es paralela al eje Y. Las soluciones de 0 x 4 son los puntos entre el eje Y y la recta x = 4
- La recta r : y = 4 pasa por el punto (0,4) y es paralela al eje X. Las soluciones de 0 y 4 son los puntos entre el eje X y la recta y = 4
- La recta t : y = x/2 pasa por los puntos (0,0) y (2,1) . Las soluciones de y x /2 son los puntos de su izquierda.
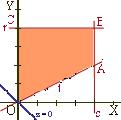
Resolviendo los sistemas correspondientes calculamos los vértices de la región factible:
{ y = x/2 , x = 0 } nos da el vértice O(0,0)
{ x = 4, y = x/2 } nos da el vértice A(4,2)
{ x = 4 , y = 4} nos da el vértice B(4,4)
{ y = 4 , x = 0 } nos da el vértice C(0,4)
2) Representamos las rectas de nivel :
En nuestro caso son rectas de la forma x + y = k . Inicialmente representamos Z = x + y = 0 . Trasladándola hacia la derecha, obtenemos las rectas : x + y = 2, x + y = 4, x + y = 8 , es decir aumenta el nivel.
3) Obtenemos la solución óptima:
Se obtiene en el punto de la región factible que hace máximo k. En nuestro caso esto ocurre en el punto B; es el último punto de contacto de esas rectas con la región factible, para el que k = 8.
Si hay dos vértices, P y Q, que se encuentran en la misma recta de nivel ,de ecuación ax + by = k .Es evidente que todos los puntos del segmento PQ son de esa recta; por tanto, en todos ellos f(x,y) vale k. Así pues, la solución óptima es cualquier punto de esa recta; en particula.
PROBLEMA METODO GRAFICO
Los 400 alumnos de Tercer y Cuarto año de Zamorano van a ir de excursión a la comunidad de Winope. Para ello, la zamoemoempresa de Desarrollo rural y ambiente contratara para el viaje a una empresa que dispone de 8 autobuses con 40 plazas y 10 con 50 plazas, pero sólo de 9 conductores para ese día. Dada la diferente capacidad y calidad, el alquiler de cada autobús de los grandes cuesta 80,00 Lempiras y el de cada uno de los pequeños, 60,00 Lempiras. ¿Cuántos autobuses de cada clase convendrá alquilar para que el viaje resulte lo más económico posible
Planteamiento:
x--------autobuses de 40 plazas
y--------autobuses de 50 plazas
max: 80,00y+60,00x
x+y<=9
40x+50y<=400
x>=0
y>=0
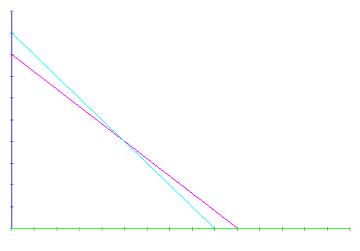
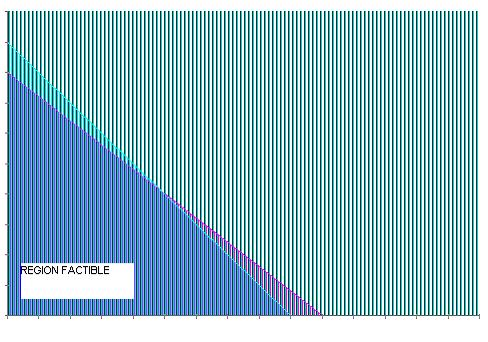
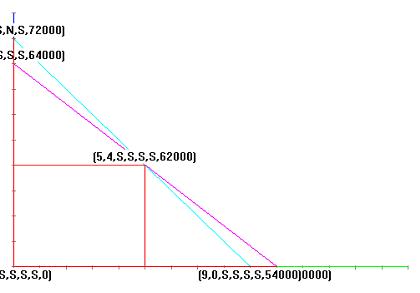
F(0, 0) = 0; S S S S Donde todo S significa que esta dentro de los parámetros
F(0, 0) = 0; S S S S
F(0, 8) = 640; S S S S
F(0, 9) = 720; S S N S ..No esta dentro las restricciones
F(0, 0) = 0; S S S S
F(10, 0) = 600; S S S N ....No
F(9, 0) = 540; S S S S
F(0, 8) = 640; S S S S
F(10, 0) = 600; S S S N No
F(5, 4) = 620; S S S S
F(0, 9) = 720; S S N S ..No
F(9, 0) = 540; S S S S
Max(0, 8) = 640
Mín(0, 0) = 0
Minimo real(9,0)= 540
La zamoempresa solo contrara los buses de 40 plazas por que solo le costara 540 lempiras en total
PROBLEMA DE LA DIETA
En Agroindustria se da una dieta "para engordar" pollos con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado sólo se encuentran dos clases de compuestos: el tipo X con una composición de una unidad de A y cinco de B, y el tipo Y, con una composición de cinco unidades de A y una de B. El precio del tipo X es de 10,00 Lempiras y el del tipo Y es de 30,00 Lempiras. Se pregunta:
¿Qué cantidades se han de comprar de cada tipo para cubrir las necesidades con un coste mínimo ?
Podemos organizar la información mediante una tabla:
|
|
Unidades |
Sustancia A |
Sustancia B |
Coste |
|
Compuesto X |
x |
X |
5x |
10,00x |
|
Compuesto Y |
y |
5y |
Y |
30,00y |
|
Total |
|
menor 15 |
menor 15 |
10,00x + 30,00y |
La función objetivo del coste total, f, si se emplean x kg del compuesto X e y kg del compuesto Y, es :
Z = f(x,y) = 10,00x + 30,00y
El conjunto de restricciones es: x >=0 , y >=0 ; x + 5y <=15 ; 5x + y <=15 .
Con estos datos representamos la región factible y las rectas de nivel de la función objetivo.
De todas las rectas de nivel que tocan a la región factible, hace que el coste Z sea mínimo la que pasa por el vértice A(2.5,2.5).
La solución óptima se obtiene comprando 2.5 unidades de X y 2.5 unidades de Y.
El coste total es : Z = f(2.5,2.5) = 10,00·2.5 + 30,00·2.5 = 100,00 Lempiras.
 |